機械学習やディープラーニングの領域において、シグモイド関数は中心的な役割を担ってきました。この記事では、Pythonを使用したシグモイド関数の実装から、その数学的背景、応用例、さらにはパフォーマンス最適化についてまで詳しく解説します。
初心者から経験者まで、シグモイド関数に関するあらゆる知識を身につけるための包括的なガイドとしてお役立てください。
シグモイド関数とは?
シグモイド関数は、ニューラルネットワークやディープラーニング、そして統計学の中でよく使われる非線形の関数の一つです。この関数は、実数値を取り、0から1の間の値を出力する特性があります。そのため、確率や「オン/オフ」のような2値の出力を表現するのに特に適しています。
例えば、ロジスティック回帰においては、シグモイド関数が予測結果を0から1の間の確率として返す役割を果たしています。ニューラルネットワークでも、活性化関数として使用されることが多いです。
シグモイド関数の数学的背景

シグモイド関数は以下の数式で表されます。
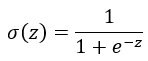
ここで、σ(z) はシグモイド関数の値、e は自然対数の底(約2.718)を表しています。
この数式をグラフにプロットすると、z の値が非常に大きいときには近似的に1に、非常に小さいときには0に近づくS字形のカーブを持つことがわかります。
シグモイド関数の特徴的なS字形のカーブは、入力の値に対して出力が飽和しない中間の範囲を持っています。この特性が、ニューラルネットワークなどでの学習中に情報を適切に伝播させる役割を果たしています。
Pythonでのシグモイド関数の実装方法

シグモイド関数は、Pythonを使用して非常に簡単に実装することができます。ここでは、基本的なPythonのコードと、効率的な計算のためのNumPyライブラリを使用した方法を紹介します。
基本的な実装
import math
def sigmoid(z):
return 1 / (1 + math.exp(-z))
この関数は任意の数値zを引数として受け取り、シグモイド関数の値を返します。
NumPyを使用した効率的な実装
import numpy as np
def sigmoid_numpy(z):
return 1 / (1 + np.exp(-z))
NumPyを使用すると、ベクトルや行列に対してもシグモイド関数を適用できます。これにより、大量のデータに対する計算が非常に効率的に行えるようになります。
シグモイド関数の導関数
シグモイド関数の導関数(微分)は、ニューラルネットワークの学習時にバックプロパゲーションを使用する際に非常に重要です。導関数は、シグモイド関数がどの程度の変化を示すかを示しています。
シグモイド関数の導関数は以下のように表されます。
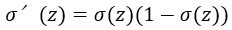
Pythonでの導関数の実装は以下の通りです。
def sigmoid_derivative(z):
s = sigmoid(z)
return s * (1 - s)
もしくはNumPyを使用した場合
def sigmoid_derivative_numpy(z):
s = sigmoid_numpy(z)
return s * (1 - s)
これにより、シグモイド関数の微分を簡単に計算することができます。この微分は、ニューラルネットワークの学習において重要な役割を果たします。
シグモイド関数の利用例: ニューラルネットワーク

ニューラルネットワークは、シグモイド関数の最も一般的な利用例の一つです。ニューラルネットワークの各ニューロンは、入力と重みを組み合わせた後、活性化関数を通して出力を生成します。シグモイド関数はこの活性化関数として使用されることが多いです。
なぜシグモイド関数はニューラルネットワークで使用されるのか?
シグモイド関数は、出力を0から1の間に制限する特性があります。この特性により、ニューラルネットワークは情報を非線形の方法で処理し、複雑な関係やパターンを学習することができます。
シグモイド関数の限界と代替手段

しかし、シグモイド関数は完璧ではありません。特に深いニューラルネットワークの学習において、いくつかの問題点が指摘されています。
勾配消失問題
シグモイド関数の最も大きな問題点は「勾配消失問題」です。シグモイド関数の出力が0または1に非常に近づくと、その導関数(勾配)の値が非常に小さくなります。これにより、ニューラルネットワークの学習が停滞する可能性があります。
代替手段としての活性化関数
シグモイド関数の限界を克服するために、様々な活性化関数が提案されています。以下はその中でも特に人気のあるものです。
- ReLU (Rectified Linear Unit): 主に隠れ層で使用され、非線形性を持ちつつ勾配消失問題を軽減します。
- tanh (Hyperbolic Tangent): -1から1の範囲の出力を持ち、シグモイド関数よりも広い出力範囲を持っています。
- Leaky ReLU: ReLUの一種で、負の入力値に対しても微小な勾配を持ちます。
Pythonライブラリでのシグモイド関数の利用

Pythonの豊富なライブラリ群の中で、シグモイド関数は機械学習やディープラーニングのフレームワークで頻繁に利用されています。
TensorFlow
Googleが開発したオープンソースの機械学習フレームワーク、TensorFlowには、シグモイド関数が組み込まれています。
import tensorflow as tf
x = tf.constant([-1.0, 0.0, 1.0])
y = tf.sigmoid(x)
PyTorch
PyTorchもまた、シグモイド関数をサポートしている人気のあるディープラーニングフレームワークです。
import torch
x = torch.tensor([-1.0, 0.0, 1.0])
y = torch.sigmoid(x)
scikit-learn
ロジスティック回帰などの機械学習アルゴリズムに使用されるシグモイド関数も、scikit-learnライブラリに実装されています。
シグモイド関数の実用例: ロジスティック回帰

ロジスティック回帰は、シグモイド関数を核とする分類アルゴリズムの一つです。名前に「回帰」とありますが、主に2値分類問題に使用されます。
ロジスティック回帰では、特徴量と重みを組み合わせた線形の結果をシグモイド関数に通し、0から1の間の確率として出力します。この出力値を閾値(多くの場合0.5)と比較して、分類結果を決定します。
Pythonのscikit-learnライブラリを使用すれば、ロジスティック回帰のモデルを簡単に実装できます。
from sklearn.linear_model import LogisticRegression
# データの準備
X_train, y_train = [...], [...]
# ロジスティック回帰モデルの学習
clf = LogisticRegression()
clf.fit(X_train, y_train)
この方法で、シグモイド関数を背後に持つロジスティック回帰モデルを容易に訓練することができます。
シグモイド関数を応用した深層学習モデル
深層学習、特にディープニューラルネットワーク(DNN)において、シグモイド関数は活性化関数として初期に多用されました。しかし、DNNの層が増えるにつれて、前述の「勾配消失問題」の影響が大きくなり、学習の難しさが顕著になりました。
シグモイド関数とDNN
シグモイド関数の持つ非線形性は、DNNが複雑な関係やパターンを捉える上で必要不可欠でした。それにより、画像や音声といった高次元のデータにおいても、特徴の階層的な表現を学習することができるのです。
Pythonとシグモイド関数: パフォーマンスの最適化

シグモイド関数は、その計算が比較的シンプルであるため、Pythonでの実装も容易です。しかし、大量のデータや層を持つDNNを扱う場合、パフォーマンスの最適化が不可欠となります。
NumPyを使用した最適化
PythonのNumPyライブラリは、ベクトルや行列計算を高速に行うための機能を提供します。シグモイド関数の計算も、NumPyを利用することで劇的に高速化することができます。
import numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x))
この実装は、大量のデータに対しても効率的にシグモイド関数を計算できます。
GPUアクセラレーションの利用
深層学習フレームワークの多くは、GPUの計算能力を活用して、シグモイド関数を含む数多くの演算を高速化しています。特にTensorFlowやPyTorchでは、簡単な設定変更だけでGPUを利用することができます。
まとめとシグモイド関数の今後の展望

この記事を通じて、シグモイド関数の基本的な性質、Pythonにおける実装方法、深層学習やロジスティック回帰での応用例、そしてパフォーマンスの最適化手法について学びました。シグモイド関数は、機械学習からディープラーニングのフィールドにおいて中心的な役割を果たしてきました。
シグモイド関数の展望
しかし、技術の進化は止まることを知りません。シグモイド関数の勾配消失問題を克服するために、ReLUやその派生形など、新しい活性化関数が提案され続けています。このような新しい関数が、深層学習の更なる進化を牽引していくことでしょう。
しかしそれにもかかわらず、シグモイド関数の理解は、多くの機械学習アルゴリズムやニューラルネットワークの背後にある基本的なメカニズムを掴むうえで非常に有益です。
今後の展望
技術の進歩とともに、新しい関数や手法が登場しても、シグモイド関数のような基本的な要素の理解が、次世代のアルゴリズムや手法を学ぶ上での基盤となります。これからの機械学習やディープラーニングの発展に目を向け、シグモイド関数の持つ普遍的な価値を見失わないことが大切です。

