データサイエンスの世界では、異なる尺度のデータを比較・分析するために「特徴量の正規化」が不可欠です。このプロセスは、機械学習のモデルが効率的かつ正確に学習するための鍵を握っています。しかし、正規化は単なる数値変換以上のものです。
正規化は、データのスケールを均一化し、モデルの性能を最適化するために用いられます。この記事では、正規化の基本から応用、さらにはその落とし穴までを深く掘り下げていきます。データサイエンスの世界での正規化の役割とその重要性を、具体的な例とともに解説していきます。
特徴量正規化の基本概念

特徴量正規化は、機械学習においてデータを均一なスケールに変換するプロセスです。異なる尺度や単位を持つデータを比較可能にするため、特徴量(データの属性や変数)を一定の範囲や形式に調整します。例えば、身長と体重のように異なる単位を持つデータを扱う際、これらを同じスケールに揃えることで、機械学習モデルの性能向上に寄与します。正規化は、データの特性を保持しつつ、モデルがデータをより効率的に処理できるようにする重要なステップです。
正規化は、データの範囲を限定することで、アルゴリズムが特徴量の重要性を適切に評価できるようにします。特に、異なる尺度のデータを扱う際には、このプロセスが不可欠です。正規化されたデータは、モデルのトレーニング時間の短縮や、過学習のリスク軽減にも寄与し、結果としてより信頼性の高い予測モデルの構築につながります。
正規化とは何か?
正規化は、データセット内の各特徴量を、通常は0から1の範囲にスケーリングするプロセスです。これにより、特徴量間の比較が容易になり、機械学習アルゴリズムがデータをより効果的に処理できるようになります。具体的には、各データポイントから最小値を引き、その結果を最大値と最小値の差で割ることで計算されます。この手法は、特に外れ値の影響を受けやすいため、データセットの特性を事前に理解しておくことが重要です。
正規化は、データの範囲を一定に保ちながら、元のデータの分布や関係性を維持することができます。これにより、特徴量間の不均衡を解消し、モデルが特定の特徴量に過度に依存することなく、全体的なパターンを学習できるようになります。
標準化との違い
標準化は、データを平均が0、標準偏差が1になるように変換するプロセスです。これは、データの平均値を引き、標準偏差で割ることによって行われます。標準化は、データの分布が正規分布に近い場合に特に有効です。一方、正規化はデータの範囲を0から1に制限することに焦点を当てています。
標準化は、データの平均値と分散を基にスケーリングを行うため、外れ値の影響を受けにくいという特徴があります。これに対して、正規化はデータの最小値と最大値を基にスケーリングを行うため、外れ値の影響を受けやすいです。したがって、データセットの特性に応じて、正規化と標準化のどちらを使用するかを選択することが重要です。
正規化の数学的原理
正規化の数学的原理は、データを特定の範囲内にスケーリングすることに基づいています。最も一般的な方法は、各特徴量の値を0から1の範囲に変換する「最小-最大スケーリング」です。これは、各データポイントから特徴量の最小値を引き、その結果を最大値と最小値の差で割ることで行われます。数式で表すと、正規化された値 ( x’ ) は以下のように計算されます。
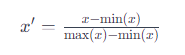
この方法は、特徴量の相対的なサイズと分布を保持しながら、異なる尺度のデータを統一的な形式で扱うことを可能にします。これにより、特徴量間の不均衡を解消し、機械学習アルゴリズムがデータをより効率的に処理できるようになります。しかし、外れ値が存在する場合、正規化の結果が大きく歪む可能性があるため、データの前処理段階で外れ値を適切に処理することが重要です。
正規化は、特に範囲が広い特徴量を持つデータセットにおいて、モデルの学習効率と性能を向上させる効果があります。また、特定のアルゴリズムでは、正規化されたデータがより良い結果をもたらすことが知られています。
正規化の重要性:なぜ必要なのか
正規化は、機械学習モデルの性能を最大化するために不可欠です。異なる尺度や単位を持つデータを同一のスケールに変換することで、モデルは特徴量間の関係をより正確に学習できます。例えば、身長と体重のような異なる単位のデータを扱う際、正規化によってこれらを同じ基準で比較できるようになります。これにより、モデルは特徴量の重要性を適切に評価し、より正確な予測を行うことが可能になります。
正規化はまた、学習プロセスを加速し、過学習のリスクを減少させます。特徴量が同じスケールにあることで、モデルはより迅速に収束し、より一貫したパフォーマンスを発揮します。特に、特徴量の範囲が広いデータセットでは、正規化はモデルの学習効率と性能を大幅に向上させることができます。
正規化は、データの前処理段階で行われることが多く、データの品質を向上させる重要なステップです。データの品質が高ければ高いほど、機械学習モデルはより正確な予測を行うことができ、ビジネス上の意思決定に大きく貢献します。
正規化の実践的応用

正規化は、機械学習の多くの分野で広く応用されています。特に、特徴量のスケールがモデルの性能に大きな影響を与えるアルゴリズムでは、正規化は不可欠です。例えば、距離ベースのアルゴリズム(k-最近傍法やサポートベクターマシンなど)では、特徴量間の距離がモデルの決定に直接影響を与えるため、正規化が重要です。
また、勾配降下法を使用するアルゴリズムでは、正規化によって特徴量のスケールを揃えることで、学習プロセスが安定し、より迅速に収束します。これは、特徴量のスケールが異なると、勾配の方向が不均一になり、最適な解に到達するのが難しくなるためです。
機械学習における役割
機械学習において、正規化はモデルの性能を最適化するための重要な手段です。特徴量が異なる尺度で測定されている場合、正規化によってこれらを同一のスケールに変換することで、モデルは特徴量間の関係をより効果的に学習できます。これにより、モデルはより正確な予測を行い、ビジネス上の意思決定に役立つ洞察を提供することができます。
正規化はまた、モデルの学習時間を短縮し、過学習のリスクを減少させる効果があります。特に、大規模なデータセットを扱う場合や、複雑なモデルを使用する場合には、正規化は学習プロセスの効率化に大きく貢献します。
データセットの例
実際のビジネスシナリオでは、顧客の購買履歴、ユーザーの行動データ、市場のトレンドなど、さまざまな種類のデータが使用されます。これらのデータは、しばしば異なる尺度や単位で測定されています。正規化を行うことで、これらの異なるデータを統一的な形式で扱い、より精度の高い分析や予測を行うことができます。
例えば、顧客の年齢と購買金額を特徴量として使用する場合、これらを正規化することで、モデルは年齢と購買行動の関係をより正確に捉えることができます。これにより、顧客の行動をより深く理解し、ターゲットマーケティングや商品の推薦などに活用することが可能になります。
正規化手法の種類
データの正規化には、複数の手法が存在します。最も一般的なのは「最小-最大正規化」と「Zスコア正規化」です。最小-最大正規化は、データを0から1の範囲にスケーリングする方法で、特にデータの相対的な位置や分布を保持するのに適しています。一方、Zスコア正規化は、データを平均が0、標準偏差が1になるように変換し、データの分布を標準化する方法です。
これらの手法は、データの特性や使用する機械学習アルゴリズムによって選択されます。例えば、外れ値の影響を受けやすいデータセットでは、Zスコア正規化が適している場合があります。また、データの範囲を0から1に限定したい場合は、最小-最大正規化が適切です。
他にも、ロバスト正規化やデシマルスケーリングなどの手法があり、これらは特定の状況やデータの特性に応じて使用されます。正規化手法の選択は、データの特性を理解し、目的に合ったものを選ぶことが重要です。
Pythonによる正規化の実装
Pythonは、データサイエンスと機械学習の分野で広く使用されており、データの正規化を簡単かつ効率的に行うことができます。PythonのライブラリであるPandasやNumPyを使用すると、データセットの正規化を数行のコードで実行できます。また、機械学習ライブラリのScikit-learnには、データの前処理を行うための多くのユーティリティが含まれており、これを利用することで、効率的にデータを正規化できます。
Pythonでの正規化の実装は、データセットの特性を理解し、適切な正規化手法を選択することから始まります。その後、選択した手法に基づいて、PandasやNumPy、Scikit-learnを使用してデータを変換します。このプロセスは、データの品質を向上させ、機械学習モデルの性能を最大化するために不可欠です。
Pythonを使用した正規化は、データサイエンスのプロジェクトにおいて、データの前処理と分析の効率を大幅に向上させます。特に、大規模なデータセットや複雑なモデルを扱う場合には、Pythonによる正規化の実装が非常に有効です。
正規化の落とし穴と対処法

正規化は多くのメリットを提供しますが、注意すべき落とし穴も存在します。最も一般的な問題の一つは、外れ値の影響です。特に最小-最大正規化では、外れ値が存在すると、他のデータポイントが狭い範囲に圧縮され、その結果、モデルの性能が低下する可能性があります。この問題に対処するためには、外れ値を事前に特定し、適切に処理することが重要です。
また、データの分布が正規分布から大きく逸脱している場合、正規化は必ずしも最適な選択ではありません。このような場合、データの変換方法を再考するか、異なる正規化手法を選択する必要があります。例えば、ロバスト正規化は外れ値の影響を受けにくいため、非正規分布のデータに適しています。
正規化のプロセスは、データの特性と目的に応じて慎重に選択し、適用する必要があります。データの前処理は、機械学習モデルの性能に大きな影響を与えるため、正規化の適用には注意が必要です。
正規化の限界と代替手段
正規化は多くの場合に有効ですが、すべての状況に適しているわけではありません。特に、データの本質的な特性やパターンを変更してしまう可能性があるため、正規化の適用には慎重な判断が必要です。例えば、時系列データや地理的データのように、データの絶対的な値が重要な意味を持つ場合、正規化は適切ではない場合があります。
このような状況では、代替手段として特徴量の変換や異なるスケーリング手法を検討することが重要です。例えば、対数変換やボックス=コックス変換は、データの分布をより正規分布に近づけることができ、外れ値の影響を軽減する効果があります。また、特定の機械学習アルゴリズムでは、正規化なしでも効果的に動作することがあります。
正規化の限界を理解し、データの特性や分析の目的に応じて最適な前処理手法を選択することが、データサイエンスプロジェクトの成功には不可欠です。
業界事例:正規化の実世界応用
正規化は、多くの業界で実世界の問題解決に応用されています。金融業界では、顧客のリスク評価やクレジットスコアリングに正規化されたデータが使用されます。これにより、異なる金融商品や顧客の属性を一貫した基準で比較し、より正確なリスク評価を行うことが可能になります。また、ヘルスケア業界では、患者の診断や治療計画の策定において、正規化された医療データが重要な役割を果たします。
小売業界では、顧客の購買履歴や行動データを正規化し、パーソナライズされたマーケティング戦略や商品推薦システムの開発に利用されます。これにより、顧客一人ひとりのニーズに合わせたサービスを提供し、顧客満足度の向上に寄与します。また、製造業界では、生産プロセスの最適化や品質管理に正規化されたデータが用いられ、効率的な生産体制の構築や製品品質の向上に貢献しています。
これらの例からもわかるように、正規化はデータ駆動型の意思決定を支援し、ビジネスの効率化と競争力の向上に大きく貢献しています。
未来のデータ処理:正規化の進化

データサイエンスと機械学習の分野は急速に進化しており、正規化の手法もまた進化を続けています。将来的には、より洗練された正規化手法が開発され、複雑なデータセットの処理がさらに効率化されることが期待されます。また、AIと機械学習アルゴリズムの進化に伴い、自動化されたデータ正規化プロセスが一般化する可能性があります。これにより、データサイエンティストはデータの前処理にかかる時間を削減し、より分析やモデル開発に集中できるようになるでしょう。
さらに、ビッグデータの時代においては、大量のデータをリアルタイムで処理するための新しい正規化手法が求められています。ストリーミングデータや非構造化データの増加に伴い、これらのデータを効率的に処理し、価値ある洞察を引き出すための正規化手法の開発が重要になってきています。
正規化は、データサイエンスの分野でのイノベーションを推進し、ビジネスや社会におけるデータの活用をさらに進化させる鍵となるでしょう。
まとめ:データの均一化と特徴量正規化の重要性
特徴量の正規化は、データサイエンスと機械学習において不可欠なプロセスです。異なる尺度や単位を持つデータを同一のスケールに変換することで、モデルは特徴量間の関係をより正確に学習し、効率的な予測を行うことが可能になります。正規化と標準化は異なるアプローチを提供し、データの特性に応じて適切な手法を選択することが重要です。
金融、ヘルスケア、小売、製造など多岐にわたる業界での正規化の応用例は、データ駆動型の意思決定を支援し、ビジネスの効率化と競争力の向上に寄与しています。Pythonをはじめとするツールを用いた正規化の実装は、データサイエンティストにとって重要なスキルです。しかし、外れ値の影響やデータの本質的な特性の変更など、正規化の落とし穴に注意する必要があります。
今後、データサイエンスと機械学習の進化に伴い、より洗練された正規化手法が開発され、大量のデータをリアルタイムで処理する新しいアプローチが期待されています。正規化は、データの活用をさらに進化させ、ビジネスや社会におけるイノベーションを推進する鍵となるでしょう。

